The Impact of the COVID-19 Pandemic on My Walking Behavior in 2020
In this post, we will take a look back at 2020, and analyze my step count data to understand some of the impacts that the COVID-19 crisis had on my walking behavior during that crazy year.
The Data
Step Counts & Measurement Devices
The step count data come from 2 sources in 2020 - I had a Fitbit for the first 8 months of the year, but it died in August. At that point, I switched to the Mi Band 5, which recorded my steps from the second half of August through the end of the year. There was a period of about 2.5 weeks where my step counts were not recorded - in between the time when my Fitbit died and when I got the Mi Band. In total, we have 345 observations of daily total step counts from 2020.
Both step count data sources are accessible (with a little work) via R: you can see my write up of how to access data from Fitbit here and my post on how to access data from the Mi Band here.
Time Period: Pre-Covid vs. Covid
The major event this past year that re-organized nearly all aspects of our lives was the COVID-19 pandemic. The pandemic and related rules and regulations shifted my movement quite a bit. Since March of 2020, for example, I have been working from home, and most of my activities have been done on foot, rather than by car.
In order to understand the differences between the pre-COVID and COVID periods, we will look at differences in step counts before the beginning of the first shutdowns of schools, restaurants, and public assembly, which occurred on March 14th, 2020 in the country where I live. All observations which occurred before this date are considered as the pre-COVID period, while all observations on or after this date are considered as the COVID period.
You can find the data and all the code from this blog post on Github here.
The head of the dataset (named daily_data) looks like this:
| date | daily_total | dow | week_weekend | device | month | time_period |
|---|---|---|---|---|---|---|
| 2020-01-01 | 16903 | Wed | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-02 | 16707 | Thu | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-03 | 18046 | Fri | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-04 | 18262 | Sat | Weekend | Fitbit | 1 | pre_covid |
| 2020-01-05 | 16172 | Sun | Weekend | Fitbit | 1 | pre_covid |
| 2020-01-06 | 12009 | Mon | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-07 | 16923 | Tue | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-08 | 11248 | Wed | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-09 | 18335 | Thu | Weekday | Fitbit | 1 | pre_covid |
| 2020-01-10 | 12539 | Fri | Weekday | Fitbit | 1 | pre_covid |
Average Daily Step Count Per Week Across 2020
One of the complicated things about visualizing a year’s worth of step count data is that there are a lot of data points - too many to plot individually and extract high-level take aways from the data. Therefore, my first analysis was of the average daily step counts per week.
The chart below shows the average daily step counts for each week of the year. I first group the data by week (automatically extracted from the date column using the lubridate package). For each week, I calculate the average number of steps per day, and also determine the month that the start of the week took place in. I then make a bar chart, displaying the averages per week across the course of the year. I color the bars according to month, and add a dashed vertial line during the week of the first COVID lockdown.
The code to produce this plot looks like this:
# set up the palette for the first plot
# using Polychrome library
library(Polychrome)
mypal <- kelly.colors(14)[3:14]
swatch(mypal)
names(mypal) <- NULL
# Plot weekly averages with color by month
daily_data %>%
# create a "week" variable from the date
# using the lubridate package
mutate(week = week(date)) %>%
# group the data by week of the year
group_by(week) %>%
# for each week, calculate the average step count
# and which month the week was in (used for color)
summarize(avg_steps = mean(daily_total),
month = min(as.numeric(month))) %>%
# turn the month variable into a factor
mutate(month = factor(month.abb[month],levels=month.abb)) %>%
# pass the data to ggplot
ggplot(data = ., aes( x = week, y = avg_steps, fill = month)) +
# set the range of the y axis
coord_cartesian(ylim = c(8000, 20000))+
# specify we want a bar chart
geom_bar(stat = 'identity') +
# draw a dashed vertical line during the week
# that the first lockdown started
geom_vline(xintercept = 11, linetype="dashed",
color = "red", size=1.5) +
# draw a dashed vertical line during the week
# of switch from Fitbit to Mi Band
geom_vline(xintercept = 32, linetype="dashed",
color = "darkblue", size=1.5) +
# annotations on plot
annotate(geom = 'text', x = 5, y = 19500,
label = 'First COVID-19 \n Lockdown',
color = 'darkred', size = 4.5) +
annotate(geom = 'rect', xmin = -1.5, xmax = 11,
ymin = 18500, ymax = 20250, fill = 'red',
alpha = .15) +
annotate(geom = 'text', x = 38, y = 19500,
label = 'Switched from \n Fitbit to Mi Band',
color = 'darkblue', size = 4.5) +
annotate(geom = 'rect', xmin = 32, xmax = 44.5,
ymin = 18500, ymax = 20250, fill = 'blue',
alpha = .15) +
# set the axis labels and title
labs(fill='Month',
x = "Week of the Year",
y = "Average Daily Steps Per Week",
title = 'Average Daily Steps Per Week: 2020') +
# specify the black and white theme
theme_bw() +
# set the colors according to the above palette
scale_fill_manual(values = mypal)And produces the following plot:
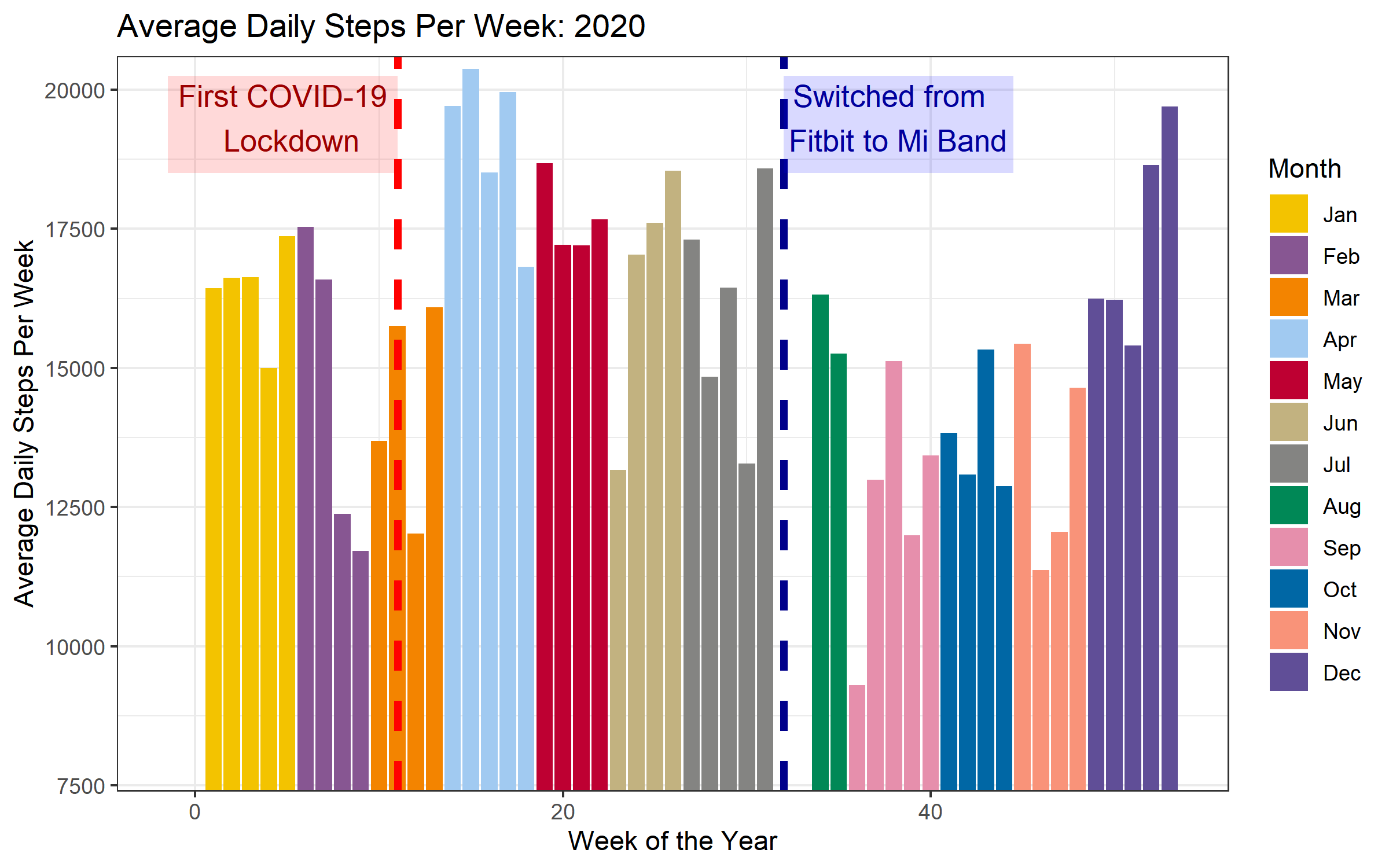
It looks like the week after the lockdown, I was walking a lot less than the previous couple of weeks. However, from the second week of the COVID period, my average step counts increased quite a bit. This matches my memory of this time period - staying inside for a week, but then going a bit stir crazy and getting outside to move around as much as possible. By this point, I was no longer commuting to work, and so it was easier to make time to get outside. The days were getting longer and the weather was nicer than normal, and I seem to have taken advantage of this in April and May.
There is a gap of 2.5 weeks at the beginning of August. As I note above, this was during the period after my Fitbit died, but before my Mi Band 5 had arrived. The step counts for September, October and November (the first months with the Mi Band) appear to be lower than those of the previous months (where the step counts were measured via Fitbit).
A Simple Model of Daily Step Counts in 2020
In order to disentangle the impact of these factors, I made a simple regression model of my daily step counts. The predictors were the various factors we have discussed so far: time period (pre-COVID vs. COVID), measurement device (Fitbit vs. Mi Band), and whether the day was a weekday or a weekend (I know from previous analyses of my steps that the patterns are quite different on weekdays and weekends).
We can run this model and request the results with the following code:
# basic regression: predict daily total from:
# time period, device, week/weekend
lm_1 <- lm(daily_total ~ 1 + time_period + device + week_weekend, data = daily_data)
# examine model results
summary(lm_1)Which returns this summary table:
| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 16150.9 | 417.85 | 38.65 | 0 |
| time_periodpre_covid | -1654.35 | 661.48 | -2.5 | 0.01 |
| deviceMiBand | -2797.26 | 556.67 | -5.03 | 0 |
| week_weekendWeekend | 3014.81 | 547.69 | 5.5 | 0 |
| Observations | 345 | |||
| R2 / R2 adjusted | 0.142 / 0.134 | |||
Lots of information to unpack here! Let’s go through the coefficients and interpret them to understand my walking patterns in 2020.
- Intercept: The intercept value is 16150.9. This is my average daily step count, when the values of all the other variables in the model are zero / at their reference categories (e.g. days during COVID, recorded with the Fitbit, and weekdays). Another way of saying this is that, on average, I walked 16150.9 steps during weekdays in the COVID period when I was measuring steps with the Fitbit.
- time_periodpre_covid: This is a dummy variable that represents the comparison between the pre-COVID and the COVID periods. The value given in the table represents the average value of the pre-COVID period compared to the COVID period. In other words, keeping all the other variables in the model constant, I walked 1654.4 steps fewer during the pre-COVID period vs. during the COVID period. In short, in 2020, I walked more during COVID than I did before the pandemic!
- deviceMiBand: This is a dummy variable that represents the comparison between measurement devices (e.g. Fitbit vs. Mi Band). The value of -2797.3 means that, keeping all the other variables in the model constant, I walked on average 2797.3 fewer steps per day when the data were recorded with the Mi Band. It is unclear whether this is due to measurement differences between the fitness trackers, or whether something changed in my walking behavior during the period when I got the Mi Band. Note that the difference between the time period (COVID / pre-COVID) is +1654 steps, whereas the difference between the devices (Fitbit / Mi Band) is -2797 steps; this means that, the bump seen during COVID (+1654) is erased when I change tracking devices (because the Mi Band average is 2797 steps lower than the Fitbit average).
- week_weekendWeekend: This is a dummy variable that represents the comparison between weekdays and weekends. The value of 3014.8 means that, keeping all the other variables in the model constant, I walked on average 3014.8 steps more per day on weekends vs. weekdays. We saw this same pattern in my previous blog post about extracting data from the Mi Band.
Note that the R squared values for this model are not very high - there is clearly a great deal of variation in my step counts that is not explained by the few predictors in our model. Let’s calculate some basic model error metrics using a function I described in a previous post:
# function to calculate model error
compute_model_performance <- function(true_f, pred_f){
# and calculate model performance metrics
# error
error_f <- true_f - pred_f
# root mean squared error
rmse_f <- sqrt(mean(error_f^2))
print('RMSE:')
print(rmse_f)
# mean absolute error
mae_f <- mean(abs(error_f))
print('MAE:')
print(mae_f)
}
# calculate the model error
compute_model_performance(daily_data$daily_total,
predict(lm_1, daily_data))This code returns the following to the console:
[1] "RMSE:"
[1] 4560.467
[1] "MAE:"
[1] 3289.286Our root mean squared error is 4560.47 and our mean absolute error is 3289.29. Not huge values in an absolute sense, but it must be noted that the MAE is around 20% of the intercept value from our above linear model (e.g. 3289/16151 is about 20%).
To get a better sense of the model performance, let’s plot out the daily observations and the model predidictions on the same graph.
We first need to add the predictions to our data set, which we can do like this:
# add the predictions to the main dataset
daily_data_predict <- cbind(daily_data, predict(lm_1, interval = 'confidence'))Our new data frame, called daily_data_predict, looks like this:
| date | daily_total | dow | week_weekend | device | month | time_period | fit | lwr | upr |
|---|---|---|---|---|---|---|---|---|---|
| 2020-01-01 | 16903 | Wed | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-02 | 16707 | Thu | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-03 | 18046 | Fri | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-04 | 18262 | Sat | Weekend | Fitbit | 1 | pre_covid | 17511.36 | 16197.24 | 18825.47 |
| 2020-01-05 | 16172 | Sun | Weekend | Fitbit | 1 | pre_covid | 17511.36 | 16197.24 | 18825.47 |
| 2020-01-06 | 12009 | Mon | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-07 | 16923 | Tue | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-08 | 11248 | Wed | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-09 | 18335 | Thu | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
| 2020-01-10 | 12539 | Fri | Weekday | Fitbit | 1 | pre_covid | 14496.54 | 13400.06 | 15593.03 |
We can now make our plot. We will plot the daily step count totals for all 345 days in our dataset, which is a lot of points - too many, in my opinion, to easily pick up the patterns revealed by the regression model we calculated above. However, we can plot the result of the model predictions on top of the points, which will show us visually what the coefficients in our above table mean. Furthermore, by comparing the distance between the points and the regression line, we can get a visual sense for the predictive performance of the model.
We can make the plot with the following code:
# set up the palette for the prediction plot
pal_2 <- c("#40830D", "#BD002E")
swatch(pal_2)
# plot the actual and predicted values
# from the regression model
# different lines weekday / weekend
ggplot(data = daily_data_predict,
aes(x = date, y = daily_total,
color = week_weekend)) +
# specify that we want points
geom_point(size = 1, alpha = .85) +
# for the predictions, we will use black crosses
# instead of points
# http://www.sthda.com/english/wiki/ggplot2-point-shapes
geom_point(aes(y = fit), color = 'black',
size = 2, shape = 4) +
# draw the predicted values and connect with a line
geom_line(aes(date, fit), size = 1) +
# set the limits of the y axis to focus on
# range where most of the data lies
coord_cartesian(ylim = c(5000, 25000)) +
# add the vertical line indicating the date
# that the first lockdown began
geom_vline(xintercept = date('2020-03-14'),
linetype="dashed",
color = "red", size=1.5) +
# draw a dashed vertical line during the week
# of switch from Fitbit to Mi Band
geom_vline(xintercept = date('2020-08-08'), linetype="dashed",
color = "darkblue", size=1.5) +
# annotations on plot
annotate(geom = 'text', x = date('2020-01-30'), y = 24500,
label = 'First COVID-19 \n Lockdown',
color = 'darkred', size = 3.5) +
annotate(geom = 'rect', xmin = date('2019-12-25'), xmax = date('2020-03-05'),
ymin = 23000, ymax = 25700, fill = 'red',
alpha = .15) +
annotate(geom = 'text', x = date('2020-09-20'), y = 24500,
label = 'Switched from \n Fitbit to Mi Band',
color = 'darkblue', size = 3.5) +
annotate(geom = 'rect', xmin = date('2020-08-10'), xmax = date('2020-10-30'),
ymin = 23000, ymax = 25700, fill = 'blue',
alpha = .15) +
# set the axis labels and title
labs(x = "Date",
y = "Daily Total Step Count",
title = '2020 Daily Total Step Count: Actual and Fitted Values',
color = 'Weekday / Weekend') +
# choose black and white theme
theme_bw() +
# scale the x axis - month tick marks
# and labelled with abbreviated month name
scale_x_date(date_breaks = "1 month", date_labels = "%b") +
# use the color palette we specify above
scale_color_manual(values = pal_2)Which returns the following plot:
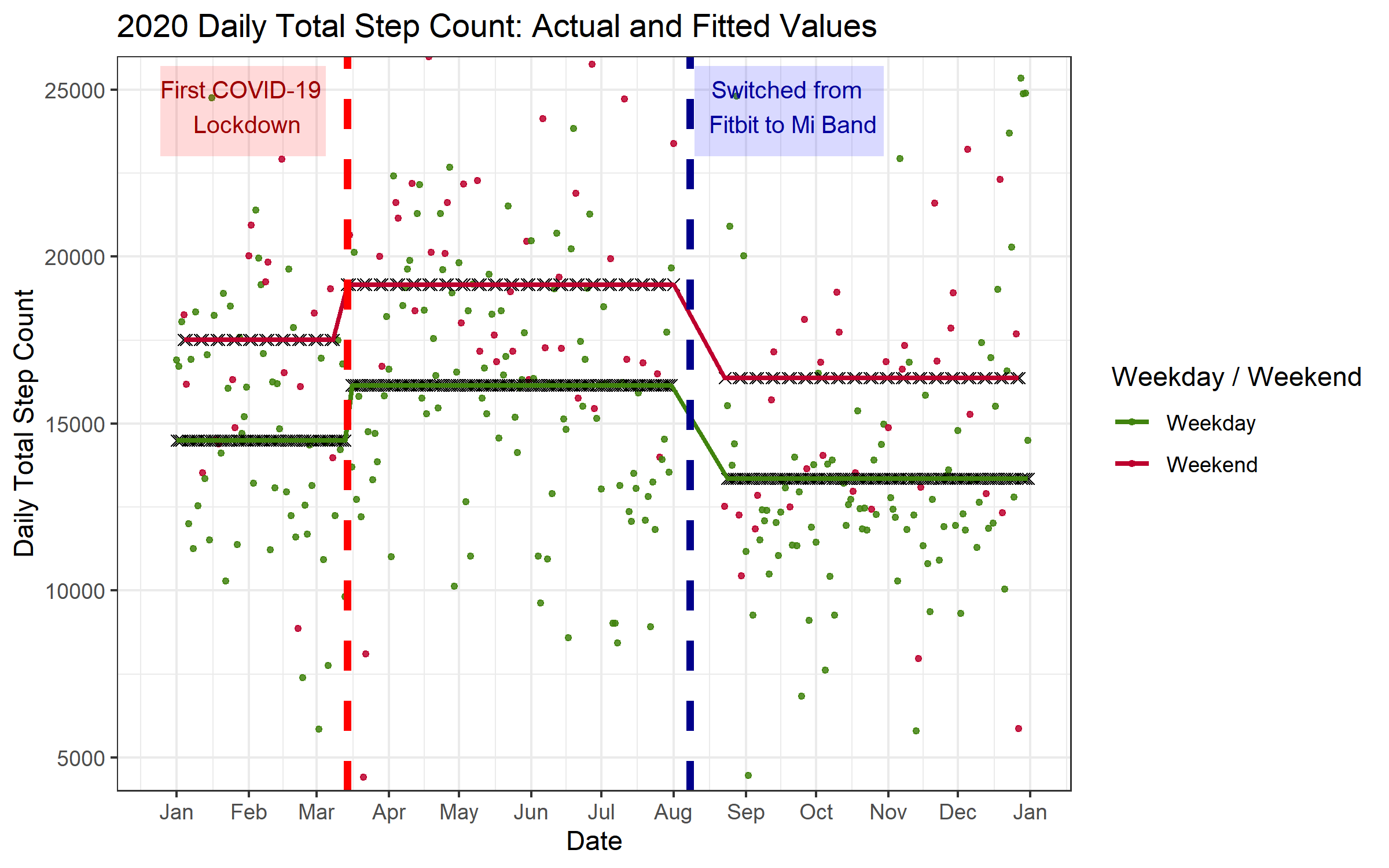
This plot is a nice complement to the regression table above. We see the impact of all of our predictor variables quite clearly. The predicted daily step count increases after the first COVID lockdown (shown, as above, with a vertical striped red line), the predicted daily step counts for the weekends (upper line, maroon color) are higher than the predicted step counts for the weekdays (lower line, green color), and the predicted daily step counts for the period where I had the Mi Band (from the end of August til the end of the year) are lower than the predicted step counts for the period where I had the Fitbit (January until July).
Furthermore, this plot gives some perspective on the model performance. The plot shows clearly the basic patterns mentioned above, but also shows there is a great deal of variation in my daily step counts that is not explained by the variables in the model (indeed, the R2 in the tables above suggests that the regression model explains only 13% of the variance in step counts). On average, our predictions are off by 3289 steps; the plot gives a visual representation of the scale of the differences between the actual step counts vs. the predictions across the entire year.
Summary and Conclusion
In this post, we used data from two different step trackers (Fitbit and Mi Band) in order to understand my walking patterns in 2020. We first looked at the daily average step counts per week across the entire year and saw indications that I walked more during the pandemic than before it. We then made a basic regression model to quantify the differences across time periods (pre-COVID vs. COVID), trackers (Fitbit vs. Mi Band) and type of day (weekday vs. weekend).
My main takeaways from this analysis are:
-
The COVID-19 pandemic seems to have had an impact on my walking behavior, such that once the pandemic started, I ended up walking more. Indeed, after the first lockdown, I stopped commuting to work and did most of my activities by foot rather than by car. Furthermore, at many points during the pandemic and resulting lockdowns, physical exercise was one of the only valid reasons to leave the house. I definitely took advantage of this and ended up walking more as a result.
-
My daily step counts were lower when I was wearing the Mi Band vs. the Fitbit. However, it’s not quite certain why. This article from Wirecutter (a review site run by the New York Times) shows the results of tests that suggest that the Fitbit I had (Fitbit HR) counts more steps than the Mi Band, so part of the difference could be due to this. However, I started wearing the Mi Band towards the end of the summer holiday period, which was followed by a return to work and the re-opening of the schools, and it’s possible that my schedule changed in such a way that I walked fewer steps during this time.
-
I walk more during the weekends than during the week days. I saw this in a previous analysis of some of these data, but this analysis of the entire year of 2020 confirms this fact. As I mentioned last time, this is a reversal from my walking patterns 4 years ago. Given that I worked from home for much of 2020, it makes sense that I walked less during the weekdays. It’s hard to accumulate many steps when your desk is 50 steps from your bedroom!
Coming Up Next
In the next post, we will analyze data from my music collection, and examine song tempos across the course of an album. How do artists sequence their albums - with fast or slow songs at the beginning, middle, or end? Is this sequencing the same or different across different music genres? We’ll explore these questions and more in the next post.
Stay tuned!